How far is the view from the top of the Eiffel Tower? That's the question this page answers, and this answer may be surprising nowadays.
Visibility limits
Nowadays when one physically rides on the tower the view is breathtaking, especially as the sky is clear. The air of Paris, rather polluted it is necessary to say it well, is not enough to allow the view to the horizon, which is 85 Kms, to answer the question directly. The elements more distant visible are:
- In the northwest, the Lyons forest, at the end of the Coudray mountain range (85 km)
- North of Clermont (60 km)
- In the North-East the forest of Compiègne (80 km)
- In the East the surroundings of Château-Thierry (70 km)
- In the South-East the plateaus of Brie, towards Provins (80 km)
- In the South the plateaux of the forest of Fontainebleau and those near Etampes (55 km)
- In the west, the slopes of Saint-Cloud and the surroundings of Vernon (65 km)
That's what visitors can actually see. But it is possible to calculate what they can see theoretically, by scholarly calculations having as constant the roundness of the Earth and the height of the tower. Here are these calculations, and their conclusions.
Calculation of the visibility length
It is easy to determine the theoretical distance at which the rotundity of the Earth allows the view to extend.
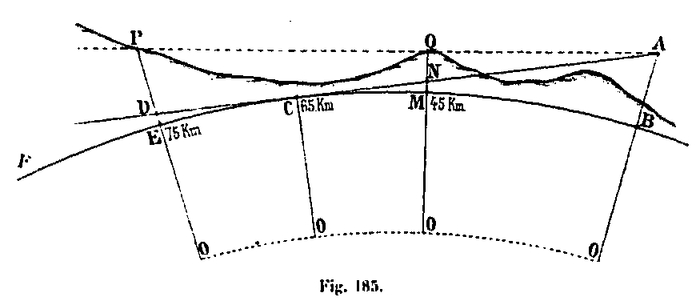
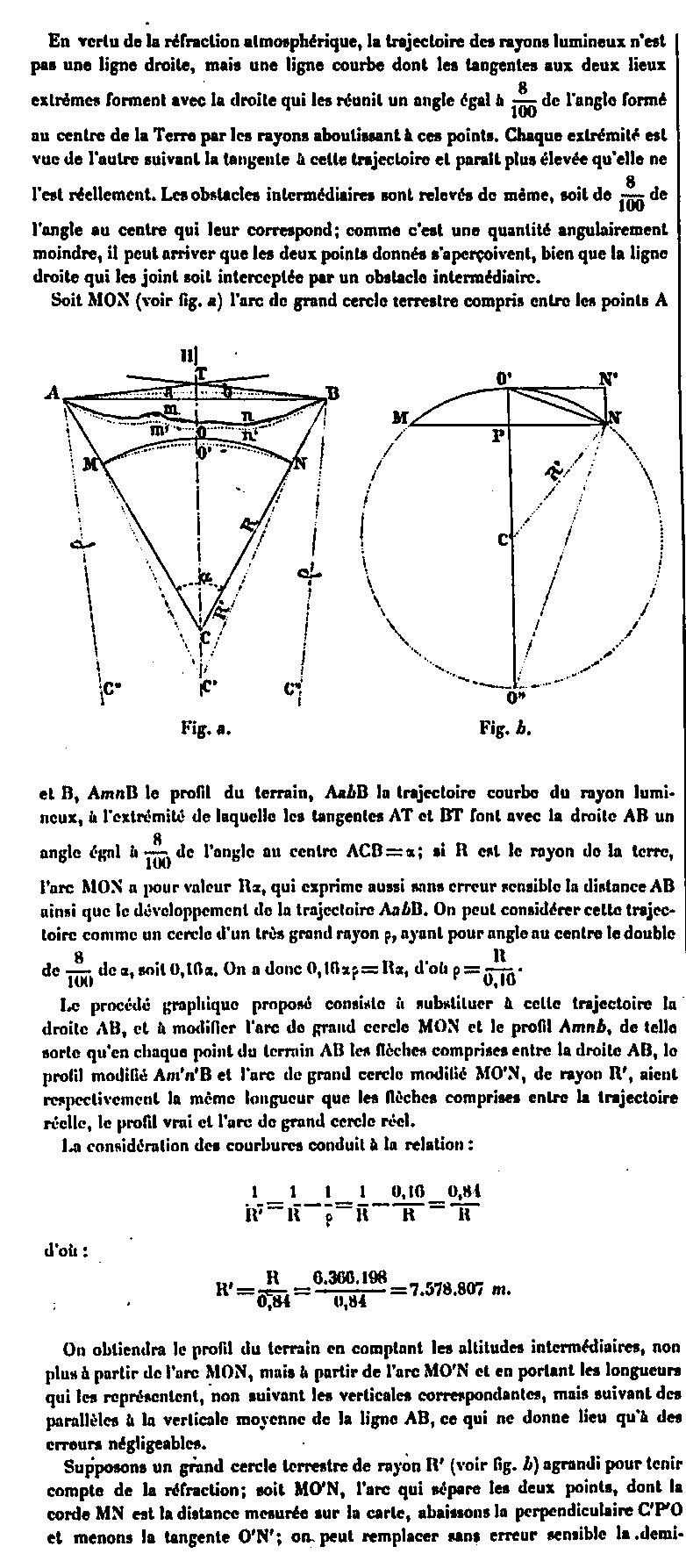
Let BF be an arc of great terrestrial circle and AB the altitude of the summit of Tower. The visual ray, starting from point A, will be tangent to this circle at point C. O being the center of the Earth, we have:
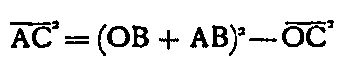
By designating the distance AC by R, the radius of the Earth OB, OC by T, and by H the altitude AB of the vertex, we have:
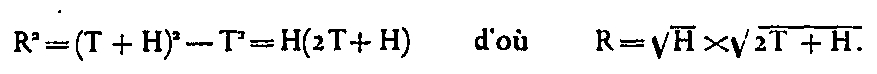
H being negligible, at least with regard to the Tower, vis-à-vis 2T = 12,732,396 m, one can ask:
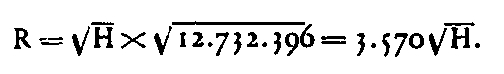
For distances of 100 Kms, where the center angle is less than 1 °, the distance R and the length of the large circle arc BC are equal. The distance of visibility can practically be calculated by this formula, when we do not take into account the atmospheric refraction of which we will study further the effects. We find, applying this formula to the main points of the Tower
- altitude of the top: H = 334
- √H = 18,27
- R = 65 224 m
- altitude of the 2nd floor: H = 149
- √H = 12,21
- R = 43 590 m
- altitude of the 1st floor: H = 91
- √H = 9,54
- R = 34 057 m
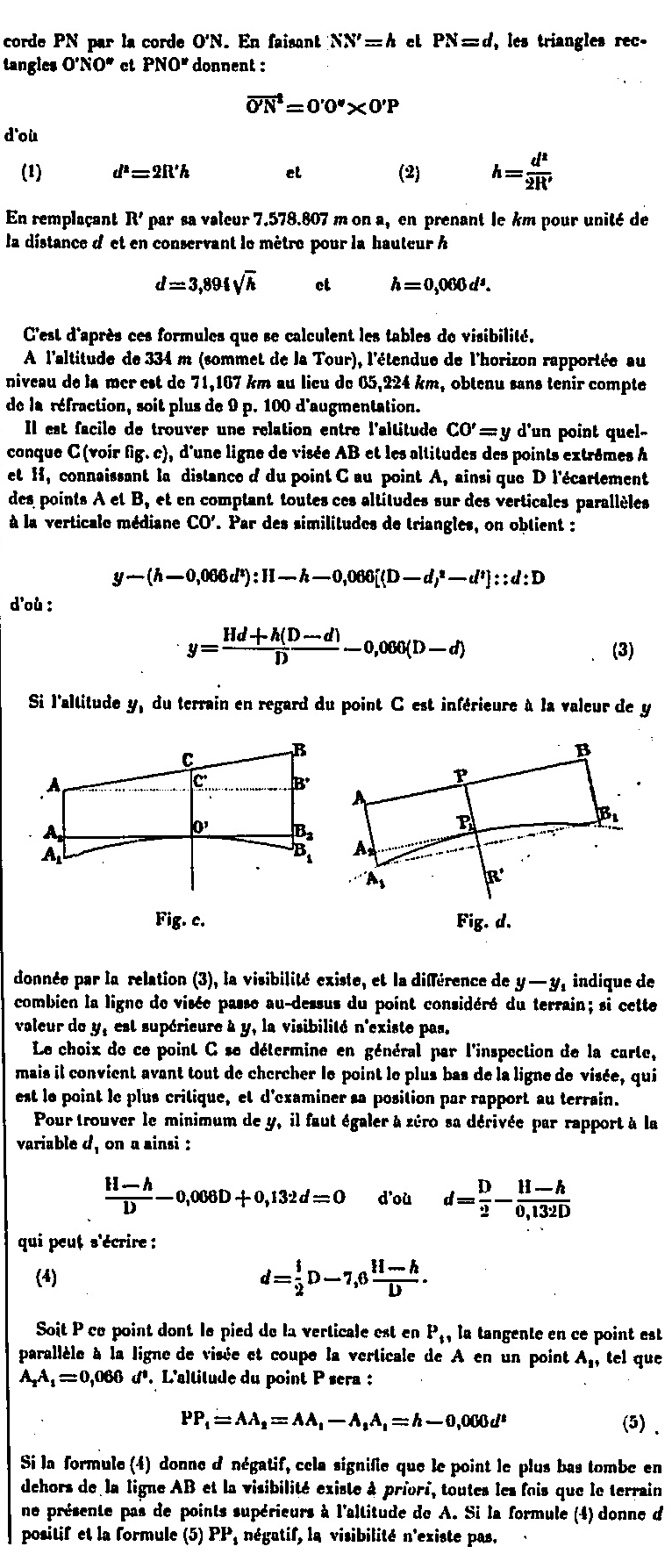
In reality, the view extends further because of the altitude of the points of the horizon, which always exceed the dimension O. If C is the point of tangency for the vertex A, all the points whose altitude as DE will take them to the prolongation of AC or above this line will be visible from the summit A. This altitude DE will be given by the same formula as before, the distance CD representing the distance beyond the point of tangency: for the distance from the point of tangency itself, we will take it equal to 65 km. If the total distances AD (or EB measured on the big circle) are 75 and 85 km, the CD differences are 10 and 20 km, and we have:
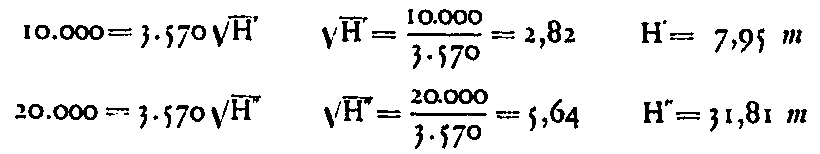
The same formula can be used to find out how far points with an altitude of 300 m are visible. We have:
rad 300 = D / 3570, hence D = 3570 x 17.32 = 61,500 m. Adding the tangential length (65 000 m), the total distance is 126 500 m.
There is therefore a chance to find points visible at 125 km among those at an altitude of 300 m and above. Conversely, the extreme range of the lighthouse (which was in place at the time, not the one currently in place) being 200 km, one can find what would be the altitude necessary to see it. We have :
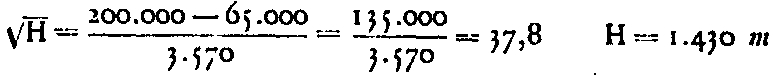
No point in a radius of 200 km from Paris has this altitude. But not only for points within the 125-km radius, but even for those in the 85-km radius, whose visibility corresponds to the low altitude of 32, this is not usually the absolute altitude who settles this question; it is especially the obstacles due to the closer vertices which form a screen above which the visual ray must pass. If a point M has an altitude MQ. which exceeds the visual radius AC, the new extreme visual ray will become AQ, which, prolonged, will cut in P the vertical passing through the point E. So that this point is visible, it will be necessary that the altitude of point E is at less equal to PE.
It is therefore necessary, in order to determine which are the points visible in each direction of the arc of great circle passing by the Tower, to make a profile in length on a length of 80 to 90 km approximately, indicating the various reliefs of the ground, and to lead the tangents from the summit to the high points. In this way we will have all the points in this direction illuminated by the lighthouse, the others remaining in the shadow. The part seen will be the set of all these enlightened points which will appear to be welded to each other without discontinuity.
In practical terms, this determination is made by the geometric methods used for optical telegraphy, taking into account the atmospheric refraction, which considerably increases the extent of visibility. We will briefly describe these processes according to two memoirs of Colonel Mangin, which the Geographical Service of the Ministry of War has kindly communicated to us. As you can imagine, these phrases are from the nineteenth century and were written by Gustave Eiffel himself, because nowadays, the Ministry of War ...

Explanation on atmospheric refraction

Explanation on atmospheric refraction

Explanation on atmospheric refraction

Explanation on atmospheric refraction
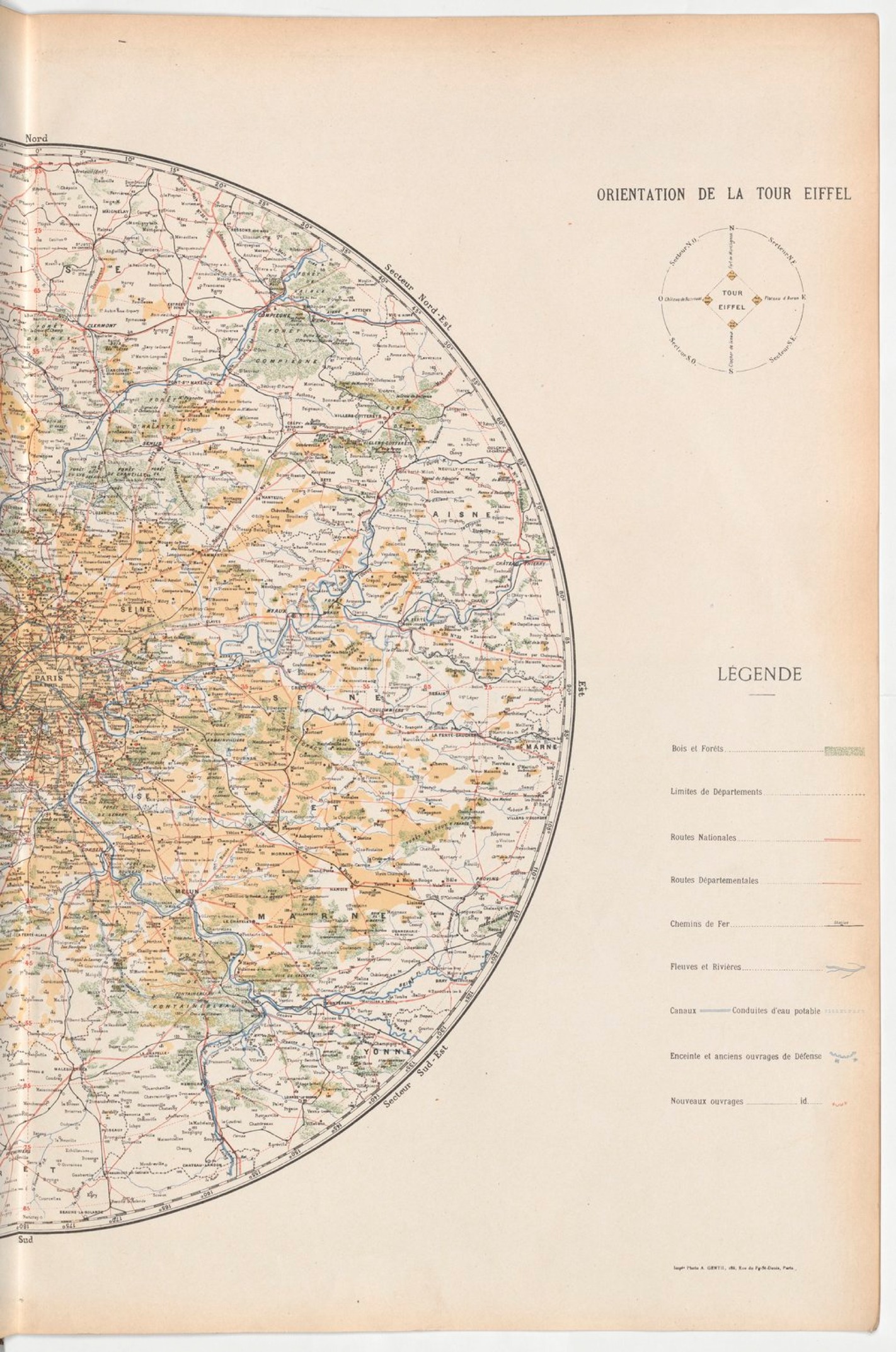
A first map to 1/320 000e was established in 1889 thanks to these processes by Mr Bourdon, civil engineer, it extended over 90 kms. A new, more complete topographic and scale of 1/200,000th was established in 1899 by Mr. Raoul d'Esclaibes-d'Hust, lieutenant-colonel of artillery in retirement and director of the service of optics of the Tower, using the results of the first card and also making the direct recognition to the telescope of a great number of points. This map, designed by Mr Fortier, is the one with the reduction to 1/400,000th shown below. It gives in yellow ocher all the visible points, the white background being preserved for the invisible parts.

Map of Paris surroundings
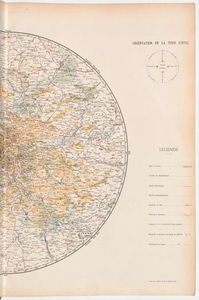
Map of Paris surroundings
See also: